The Phase Law of the Universe. Non‑Zero Distinction Axiom

Imagine a world without ‘time.’ Where everything — from sound to aging — is just phases, like frames in a film. This article is the instruction manual for a universe you never noticed.

I propose leaving behind the abstract concept of “time” as a standalone phenomenon, replacing it with measurable changes in states — phases, distinctions, and energy ticks.

This approach resonates deeply with the insights of Leibniz, Mach, and contemporary physicists such as Carlo Rovelli. You’re about to discover something that could fundamentally reshape your understanding of reality:

Everything we call “time” has always been an illusion — a placeholder for something we haven’t fully grasped yet. In this article, I won’t just argue philosophically that time is an illusion. I will show exactly how it emerges physically — as a rhythm of phase distinctions, where energy sets the tempo, the observer creates duration, and crucially, how and why it exists.

This might be the architecture of a new physics: clear, measurable, free from paradox and abstraction.

Are you ready to redefine your reality?

Space Doesn’t Need Time

Imagine you’re creating a computer game and working with 3D software. When you start a new project, what scene parameters do you set? Perhaps a title, dimensions of space, predefined lighting, colors — and now your scene is ready for creation.

Here comes the key question: Why don’t you define time parameters for the space itself?

When do you first introduce “time” into your game workflow? Only when you want something to start moving — when animation is required. This is the best example to illustrate that time isn’t what we typically think it is. We mistakenly imagine it as filling our space or existing independently, as some magical, indescribable phenomenon.

Time itself exists only as a property that enables phase changes at different dynamics.

This is precisely the essence — if there are no changes (no movement, no “other” state to compare), then saying “time flows here” is simply meaningless. “Time” appears only when we record some differences — “before → after,” or when we have at least two processes that diverge in their phases.

If we imagine a single, absolutely stationary object in the universe, with nothing to interact with and no reference points, where exactly does “time flow”? Nowhere. It becomes irrelevant for any calculations or comparisons — without changes, there are no “clocks.”

Moreover, imagine in your game scene, objects are moving at different speeds: some slowly, some rapidly, and suddenly you decide the overall pace is still too slow. You adjust a parameter controlling general movement speed.

A rhetorical question arises: Where, then, is this magical “time” or what we call time located? Within which object? Or does the entire scene define “time,” and if so — what exactly does it determine? Only the speed of phase differences. There is no absolute “timer,” and no one can declare any one tempo as the singular truth, apart from the universally indistinguishable zero-phase of the universe.

A Simple Explanation: How We Invented Time

We started from absolute stillness. Imagine you wake up in a strange world where:

• There is no time. Everything is frozen.
• You don’t yet have concepts like “fast” or “slow”.

Then you decide to move, and here’s what happens:

You wave your hand in front of your face and notice a difference between “before” and “after.” With your movement, you distinguish yourself from the space around you, realizing you’re separate from that space. This is essentially the simplest way to define a clock frequency.

This moment, when you become aware something has changed, marks the very first phase difference.

Conclusion: Movement creates differences. Without movement, there are no differences and therefore no time.

Problem: How do we measure these differences?

Imagine running one meter. You might think: “It took me N phase differences to move from point A to point B.”

But it’s not practical to say, “I’ll arrive after 10,000,000,000 phase differences!”

We noticed the sun was conveniently available for measuring phases and determining how much we can accomplish within these intervals. It was as if nature itself set predefined rules for rhythm, giving us a hint on what to base our measurements.

We began correlating the number of tasks and distances we could complete while the sun completes its cycle. Saying, “I’ll arrive after two sunsets,” became much simpler. Essentially, we started measuring everything relative to the sun. We even invented sundials and hourglasses, strongly supporting the idea that time is a set of intervals measured relative to one object against another. These intervals can manifest in countless forms and phenomena, as long as their rhythm and speed remain constant.

Conclusion: Time isn’t magic — it’s simply comparing one change against another.

Methods for improving our spatial orientation and synchronizing the rules of phases didn’t stand still. Eventually, we moved on to using cesium as a global reference. We called this device a “clock,” displaying seconds, minutes, and hours. We didn’t invent time; we didn’t discover it either.

We merely started measuring everything in “cesium phases.”

Why Cesium? Because It’s More Accurate Than Earth

Previously, a second was defined by Earth’s rotation. However, we discovered that Earth’s rotation is gradually slowing down due to tidal effects. Cesium atoms oscillate with remarkable stability, having an error margin of only one second in about 300 million years.

What does this mean?

When we say “10 seconds have passed,” it actually means: “91,926,317,700 oscillations of a cesium atom have occurred.”

If somewhere “time slows down” (like near a black hole), it actually means “cesium oscillations are occurring slower compared to our clocks.” It’s important to understand whether a black hole affects all processes uniformly. If it does, entering such an area doesn’t literally stop time; it merely slows down the rate at which phases change.

Fewer phases mean less energy expenditure. Less energy used means an object can remain longer in space, further from the point of its own “decay.”

Our universe is effectively a “zero point.” This true state is universal and can synchronize everything, and at that absolute point no “time” is perceived, since there’s no movement — no phase differences.

Simply put, true “time” is the absence of phase differences. When we say “time passes,” it means phase differences have occurred. When we say “time stands still,” it means nothing is literally moving. That’s why people intuitively say they feel as if nothing changes in their lives when things remain static. Thus, time itself is actually a series of phase differences. The genuine “time” is zero! Without zero, we couldn’t measure anything. All “movement” in time, all initial phases, start from zero!

For “time” to occur, we must move out of zero: initiate changes (movements, processes) at some speed.

Parallel processes (with varying frequencies or speeds) enable observers to record differences over time, stating things like: “One object moves faster, another moves slower.” If everything operated at identical rates or remained completely motionless, no differences — no “flow” — would be observable.

Simple truth:

We took an external cycle — Earth’s rotation around the Sun. We counted how many cesium oscillations happen during this cycle and obtained about 794 trillion. These 794 trillion oscillations we named a day, or 24 hours.

Because oscillations occur regularly, we simply divided them into convenient portions: hours, minutes, and seconds, making counting and comparison easier. Clock hands returning repeatedly to the same position isn’t magic. It’s simply a point of resonance, geometric synchronization of phases, indicating the cycle is complete and ready to restart. This entire process we created to count phases, label them, divide, and synchronize is what we call “time.”

In reality, this “time” is not an independent entity. It’s simply a rule, a counter, an algorithm for aligning phase differences. The truth is, this “time” can be anything — it depends solely on which rhythm or cycle we build upon.

If time is a tool, it can be reinvented. For example:

• Martian time with days lasting 24.6 hours (or other subdivisions).
• Alternative chronometries like “biological time” based on metabolism or “computer time” measured in processor ticks.

But that’s just the tip of the iceberg — let’s dive deeper!

Time is the measurement of phase changes in a system relative to a chosen standard (like cesium).

Time is essentially a kind of rhythm, speed, relativity, synchronization — a combination of phenomena allowing phase differences to exist. Just as a clock signal in a processor synchronizes operations, time represents the rhythm of changing states (phases) in the Universe.

Any “time” measurement involves comparing one change against another (for example, Earth’s rotation around the Sun versus atomic clocks). Each object can possess its own clock frequency.

A player with adjustable playback speeds (analogy)

Imagine having a video or audio file containing all frames (or sounds) from beginning to end. The entire movie is “recorded,” complete with all details.

How we watch: We can play this video:

• At normal speed (1×)
• Faster (2×, 5×)
• Slower (0.5×, slow-motion)

So where exactly is this mysterious “time” filling our space, if we can easily manipulate it within our media player?

Analogy:

All “ticks” (frames, beats per minute) already exist, just as they do in the “structure of reality.”

We, as observers, decide how fast we “play” these frames through our perception.

Imagine a long track with marks drawn at regular intervals: every 1 meter, 2 meters, 0.5 meters — doesn’t matter. This is similar to how “all coordinates” already exist in space’s geometry.

All “markings”:

• Represent “all possible positions” you can occupy.
• The track doesn’t spontaneously form beneath your feet; it’s already fully laid out.

You can:

• Walk slowly (using little energy) and pass 1 meter in a minute.
• Run (more energy), passing 1 meter in 5 seconds.
• Ride a bicycle (faster still).
• Drive a car (even faster).

Time is simply a convenient tick to count changes. There are no universal clocks — only standards we’ve agreed upon.

“Time” Has Nothing to Do with Your Aging

It’s not time itself that “kills” you, but rather the processes inside your body.

Aging is about your body’s natural initial reserve of “energy,” which gradually gets used up. You can use this reserve quickly or slowly. You can replenish your energy or rapidly expend it. Some factors are within your control, others are not. Aside from external influences like viruses and diseases, your internal “clock” depends entirely on how quickly you consume your energy reserve, how well you conserve it, and how you live your life.

What happens as you age:

• Basal Metabolic Rate (BMR) decreases
• Your body consumes less energy at rest because it shifts into energy-saving mode. Your initial energy reserve diminishes gradually.
• Mitochondrial activity declines
• Cellular respiration efficiency worsens.
• ATP production (energy molecules) decreases.

You literally slow down because cells and molecules in your body contain less and less energy. Eventually, the decay phase begins. It’s not “time” killing you, but natural laws: everything eventually decays. Possibly the only exception is consciousness, provided we learn to replace our “biological bodies.”

Ultimately, everything boils down to energy and your ability to produce a certain number of “phases” within a specific period.

How to Understand “Interstellar” Through Phase Changes

Gravity (such as Gargantua’s in “Interstellar”) curves spacetime, slowing down all processes for an external observer.

But for Cooper himself, nothing changes: his heart beats normally, neurons fire as usual, because all processes within his frame of reference slow proportionally to the surroundings.

Paradox:

He doesn’t feel slowed down, yet when returning to Earth, he discovers his phases (the years he lived through) don’t match Earth’s phases.

This is comparable to one person watching a video at 0.5× speed and another at 1× speed. The video itself doesn’t “know” at what speed it’s played, but the difference is evident when comparing the experiences of two observers.

Why doesn’t the protagonist feel any difference? Because nothing has changed from his internal perspective. It’s like resizing a shape while maintaining proportions — a square remains a square. Changes can only be observed in comparison with another shape or different dimensions.

But since the Universe serves as an external observer, what does it see? It sees one person remaining on Earth, whose phases progress at the Universe’s normal tempo, and another person near the black hole, whose phases slow down. The Universe perceives two objects: one moving quickly and another slowly — similar to observing a fast-moving car and a slow-walking pedestrian. Objects isolated within their own reference frame might not feel this change, as everything around them slows proportionally: cellular movements, internal processes, physical laws — everything.

Imagine a video clip. The video itself, composed of phases (frames), doesn’t know at which speed it’s being watched. To perceive what we call “time,” we need differences in phases and relativity. Simply put, to realize if you’ve slowed down or sped up, you need a reference point.

For instance, if the protagonist in “Interstellar” had used the rotation of the solar system as a reference (assuming it wasn’t affected by gravitational slowing), he would notice that as he approached the black hole, the solar system appeared to rotate faster, indicating that he had slowed down. To match Earth’s phase of time again, he’d need to adjust his phase speed to match the solar cycle — where half the cycle is spent sleeping and half awake. This doesn’t represent different spaces but different activity levels within the same plane of the Universe.

Imagine placing two pieces of frozen meat from your freezer — one in a microwave, another on a table. The first defrosts in 10 minutes, the second in 10 hours. For both, it’s essentially one process — they both simply defrost, each completing their predetermined sequence of phases. Only you, as an external observer, can perceive which occurred quickly and which slowly.

Only with an external reference can we detect acceleration or deceleration clearly.

How the Activity of Phase Changes Influences Animal Longevity

I became curious: if everything in the world depends on the activity of phase changes, and if a clear relationship exists between speed, strength, endurance, and other characteristics, what could this imply about animal longevity?

Whales and turtles live the longest among animals on our planet. Without diving deeply into the biology of animals and taking just one parameter — heart rate — I created a small table of various animals and found a clear correlation between longevity and heartbeat rhythm.

Of course, pulse rate is only one marker. Far more critical factors include metabolic scaling, oxidative stress resistance, telomere shortening rate, and evolutionary “life strategies.” It’s a combination of these factors. Still, this doesn’t negate the overall trend tied to the speed of phase changes.

Even if an animal has a rapid heart rate but lives longer compared to another animal, it likely has other processes functioning at slower rates. For example, bats have an overall lower “heart-beat count” due to extended phases of ultra-low heart rate, and, crucially, their molecular aging mechanisms (oxidation, inflammation, telomere wear) are slowed significantly. That’s why bats live several times longer than rodents of similar size, despite having much faster heartbeats during flight.

Plants Literally Adjust Their Phase Activity According to the Season

Looking into botany through the lens of phase changes, similar patterns emerge.

What happens to plants’ metabolism in winter:

In woody plants (deciduous trees, shrubs):

• Photosynthesis stops. Leaves — the main organ of photosynthesis — fall to prevent energy and water loss.
• Respiration (catabolism) slows down. Cells consume minimal energy, just enough to survive.
• Growth stops entirely. All energy is preserved, avoiding cellular division or formation of new tissues.
• Sugars accumulate as “antifreeze.” Certain plants gather soluble sugars and proteins that protect cells from freezing.
• Dormancy sets in — a kind of “hibernation” for plants.

Not all plants completely halt photosynthesis — conifers still photosynthesize at a very slow pace, even in frost conditions.

Just like bears:

This results from evolution — tens of thousands of years adapting to seasonal famine and cold.

Bears “learned” not to fight the cold but to wait it out, conserving fuel (energy) and minimizing their internal phase changes. Bears don’t cool to zero: their strategy moderately reduces body temperature while drastically cutting down metabolism and energy expenditure.

Then why do humans die from the cold?

We don’t have the ability to significantly slow down processes in our bodies:

• Our bodies must maintain a stable internal temperature (~36.6°C).
• Severe cooling → temperature drops → enzymatic reactions slow → body functions decline.
• Below ~28°C, the heart can stop; the brain ceases functioning.

Our cells are extremely sensitive to freezing:

• Water inside cells freezes → ice crystals damage membranes → cells die (as seen in frostbite).
• The human body can’t simply “pause and wait”; it either functions or it doesn’t.

Why can plants survive cold conditions?

Plants are dormant organisms. They don’t need to maintain a constant temperature. In winter, their metabolism almost completely stops. It’s a biological “pause,” not death. In spring, these processes resume.

Plant cells are adapted to freezing conditions:

• Remove water from cells, preventing internal freezing.
• Accumulate sugars and proteins acting as antifreeze.
• Modify their membranes to become flexible and frost-resistant.

In autumn, plants activate cold-resistance genes, strengthen cell walls, and accumulate protective substances. Some species even wind their DNA into a “winter mode.”

Yes, the slower the processes, the longer a structure — whether body, molecule, cell, or tissue — lives.

Temperature, Distance, and Other Metrics Are Just Phase Measurements — Exactly Like Time

Buckle up, because this will not only blow your mind but destroy all your illusions about the existence of any absolute measurements you learned about in school.

Now, turning to temperature, a question arises: what exactly is it at its core? As it turns out, it follows the same measurement principle as time. Temperature is simply the defined phase changes of water.

Science defines temperature as the measure of the average kinetic energy of particles. But what fundamentally underlies this “average kinetic energy”?

We observed water freezing and said: “Let’s call that zero”; boiling, we called 100. We measure everything relative to water — just as we measure time relative to cesium.

Negative values in Celsius exist simply because we chose an imperfect reference point. Water can freeze further, below our zero point. Following the same logic, we could measure distances or speeds as positive and negative relative to some arbitrary reference.

Imagine we set “safe” car driving speed at 50 km/h as our “zero.” Speeds below this could be negative (”-50 km/h,” meaning safely below the limit), and positive numbers would indicate speeding violations. We could even calculate fines directly: “You’re driving at $300 per hour.”

The Celsius scale is shifted away from the thermodynamic zero point. However, an absolute limit exists: 0 K = -273.15°C, below which classical systems can’t descend. On the Kelvin scale (0 K — absolute zero), negative values are impossible. This makes the Kelvin scale fundamentally more accurate, though less convenient for everyday use.

We Compare Everything

Imagine you have no instruments — no clock, thermometer, or ruler — but still want to determine:

• “How much time has passed?”
• “What’s the temperature outside?”
• “What’s the distance to a tree?”

The more closely you look, the clearer it becomes that these three questions reduce to one common principle: “How do we correlate changes in one thing with changes in another?”

Temperature: Merely phases of particle movement in water

The Celsius scale (0°C, 100°C) was created by observing water:

• 0°C = water freezes.
• 100°C = water boils.

Initially, temperature seems inherently real. But without water and its phase transitions, we wouldn’t know what “0” or “100” means.

Even the universal Kelvin scale is based on “energy of particle movement” (in a broader sense). But measuring this energy always requires a process — such as touching a thermometer and waiting for equilibrium, or analyzing radiation spectra.

Thus: Temperature equals the intensity of phase changes (chaotic movements) in a substance, relative to another substance. We invented the scale by comparing these changes to standard transitions (freezing/boiling water) or fundamental energy laws.

Any phase transition is not merely a shift from one state to another. It is an exchange: a new phase is always paid for with energy, order, or stability. The faster an object or phenomenon changes phases, the quicker it depletes its resources, and the shorter its lifespan becomes. This is why a whale’s heart beats slowly, allowing it to live long, while a hummingbird’s heart flutters rapidly, granting it a far briefer existence. This is not a metaphor — it is a direct consequence of the law of energy conservation, operating at all levels of reality

Distance

You might think millimeters, centimeters, meters, kilometers are absolute, existing independently in space, similar to how we previously thought about time and temperature. This myth quickly dissolves when you have to create your own ruler from scratch.

What exactly is distance?

1 meter = the distance light travels in vacuum in 1/299,792,458 seconds.

We’re essentially measuring everything by the speed of light. For many, this isn’t a revelation. However, what is remarkable is realizing that everything we call time, temperature, distance, is merely a relationship between phases — not something existing independently in space. Behind all measurements stands a specific substance, state, and phase distinction.

Conclusion: No phase changes — no measurements

• “Time” becomes meaningless without phase differences.
• “Temperature” is meaningless without the energy of phase differences.
• “Distance”? If there’s no observer or way to take steps, distance is undefined without phases.

These “quantities” aren’t absolute “things” but agreements on how we measure changes.

Therefore, talking about “traveling into the future” is as meaningless as saying you’re going to “tomorrow’s temperature.” These are consequences, not directions.

The Law of Phase Synchronization

The law of phase synchronization that I discovered supports the idea of the Big Bang theory, where all atoms began from a single unified point. This point represents synchronization itself.

Even if elements move at different speeds (In the cycle), they inevitably meet in a common phase — this is unavoidable.

What can you see in the video below?

There are 24 squares. They all start simultaneously, and their logic of movement is simple:

• The first square moves at a speed of 1 phase change.
• The second square moves at 2 phase changes.
• The third square moves at 3 phase changes, and so forth.

Their speed doesn’t vary; movements are cyclical, and all objects launch simultaneously.

External rules (observer’s frame) may differ — like the overall speed of the animation or its frame rate. For this algorithm, these details are irrelevant; it already exists as a complete algorithm, with everything else being just phase interpretation. Internally, the algorithm is unchanging. Differences arise only during comparisons.

The essential point: This isn’t a unified animation; these are separate columns with different animations, yet you clearly see how they behave when played simultaneously.

Remember the pendulum and ball movements? Could this simple mathematical algorithm mimic real physics?

As you can observe — yes, these squares replicate the behavior and “patterns” found in real life. The difference is simply in the algorithm; the object moves back and forth.

# Core algorithm demonstrating phase-based simulation
t = 0 # Initialize global phase time

while running:
dt = clock.tick(FPS) / 1000.0 # Time increment per frame (phase interval)
if is_playing:
t += dt # Increase phase time only when simulation is active

for obj in objects:
# Calculate the phase angle using individual and global phase speeds
angle = math.sin(t * obj["phase_speed"] * global_phase_speed)

# Compute object's position based on current phase angle
x = origin_x + obj["phase_length"] * math.sin(angle)
y = origin_y + obj["phase_length"] * math.cos(angle)

# Visualize phase relationship through lines and circles
draw_line(origin, (x, y))
draw_circle((x, y))

This simplified phase-based algorithm clearly illustrates how each object’s behavior is governed directly by phase distinctions and their frequencies, making it highly adaptable and intuitive to implement.

Classical physics typically describes phenomena such as pendulum waves through complex formulas involving string lengths and oscillation periods. However, the phase-based approach is simpler and more universal: instead of calculating precise lengths and periods, we directly define the phase relationships between objects. This method allows us to model and visualize phenomena rapidly, as demonstrated in the code example below. The essence of any oscillation or rhythm lies not in abstract string length, but in phase distinctions and their rate of change.

Curious — how does this algorithm look in circular animation?

This is mind-blowing! Does it remind you of anything?

What does Wikipedia say about this phenomenon?

A planetary alignment (or “parade of planets”) is an astronomical event where several planets of the Solar System appear in a straight line from the Sun within a range of 20–30°. They appear relatively close to each other in the sky.

The term “parade of planets” isn’t strictly scientific and is primarily used for popularization in astronomy.

The maximum proximity of celestial bodies by ecliptic longitude is called “conjunction.” If they are sufficiently close by ecliptic latitude, such configurations may result in eclipses or transits.

This phenomenon is viewed simply as some astronomical occurrence. Yet, I argue this isn’t an isolated event — it’s a fundamental law of the universe.

The Law of Phase Changes (Simplified)

My theory explains it this way:

• All planets (or matter from which they originally formed) shared an identical starting point.
• Planetary movements are cyclical, allowing us to observe synchronization between objects.
• This synchronization is driven by internal progressions of relativity.

Of course, in reality, this doesn’t operate as ideally as digital calculations. But clearly, if the Universe were dominated by chaotic noise without internal regularities, we’d never observe phenomena such as:

• Planetary alignments (periodic alignments).
• Orbital resonances (for instance, the 1:2:4 resonance among Jupiter’s moons).
• Atomic spectra (distinct emission lines, rather than random bursts).
• Crystal lattices (atoms synchronized into structured formations).

Without such oscillations, phases within the Universe would generate indistinguishability — like identical solar systems or other structures.

Any system with multiple frequencies inevitably synchronizes, provided the noise remains below a certain stability threshold.

If the Universe is discrete (composed of minimal indivisible “building blocks” of space, time, and energy), it radically shifts our understanding of reality.

The Universe doesn’t run on “time” — but on internal geometric patterns of distinguishable phases.

If the Universe is discrete and my theory is correct, then:

• Quantum gravity must account for phase resonances.
• Dark matter could be “noise” outside synchronized patterns.
• Future AI could model the Universe as a digital system.

Movement of Objects and the Nature of Reality: How Frequency of Perception Creates Our World

The human brain functions as a biological “phase difference detector,” operating within a strictly limited frequency range. The brain processes information discretely, with characteristic temporal delays:

Vision:

Maximum distinguishing frequency is around ~60 Hz (individual neurons can go up to 500 Hz). Movies at 24 frames per second appear smooth due to persistence of vision.

But does this imply that phases beyond our perception frequency don’t exist? Certainly not.

The simplest proof: slow-motion cameras. Phase distinctions we’re unable to detect merely occur at another frequency.

We don’t perceive “objects” directly; rather, we perceive our brain’s interpretation of their phase differences, constrained by our biology and technology.

• The human eye perceives movement as smooth flows (skipping fine details), thus causing the blur effect by missing intermediate phases.
• A slow-motion camera captures more intermediate phases missed by the human eye.
• Super slow-motion cameras capture even finer details of movements inaccessible to ordinary cameras.

Simply put:

The faster the observer (the higher their recording frequency), the more details of motion they perceive.

Photography — The Art of Capturing Phases

To capture a sharp image, photographers set the correct exposure (shutter speed) and aperture (light amount).

Why?

To synchronize parallel streams of changing phases within a single frame, because different elements within a scene move at varying speeds. To avoid blurring, the camera’s “eye” must operate faster than the phases occurring at that moment.

• If shutter speed is too slow and the object moves quickly (faster than the camera), the image will blur.
• To “freeze” fast phases (movements), shutter speed must shorten, requiring more light (otherwise, the photo will appear dark).

In night photography, we can even capture an entire sequence of phases in a single frame.

A camera visually demonstrates phase changes, how they operate, how they’re captured, and what occurs under various settings.

Analogy:

All “micro-phases of movement” already exist in reality. If we wish to capture these quick moments (frames), more “energy” is required (bright light, sensitive sensor, shorter exposure).

If insufficient light (energy) exists, we’re forced to use a longer exposure, thereby blending (blurring) rapidly changing phases.

This demonstrates clearly: the “threshold of perception” (light, energy, sensitivity) determines which rapid phases we manage to “photograph.”

The threshold of distinguishability is the border between “there is time” and “no time” for a given observer. Anything faster becomes invisible, anything slower freezes. Thus, time isn’t fundamental, but merely a function of our ability to record changes.

Example:

When driving and looking sideways, at a certain speed, objects blur. Your perception threshold is insufficient at that speed to capture changes. Perhaps, in the future, people may enhance neuronal processing to perceive faster phase changes, but currently, our biological constraints limit us.

Yet, an interesting effect occurs: if you rapidly move your eyes side-to-side while looking at a fast-moving object, you might briefly perceive a single clear frame. This happens when your eye’s speed momentarily matches the object’s speed — your perception synchronizes with its phase frequency. This effect is especially noticeable with lights or lamps.

This is why, while driving quickly, we clearly see other cars. Our phase changes synchronize with their movements relative to the static background (the road), while everything else blurs. We see the road clearly ahead because there are minimal changes directly forward. However, if you lower your eyes closer to yourself, changes occur rapidly, causing blurring. This isn’t magic; it’s the law. But the balance of these phenomena allowing us to drive safely at high speeds remains a marvel.

Looking at Sound from a Phase Perspective

If we begin noticing patterns of phase sequences everywhere in the world, a natural question arises: does sound also obey these phase laws? What exactly is “sound,” and how do phases manifest in it?

Without phases, there’s no wave and no sound. If air pressure never changed (perfectly flat line, without oscillations), we’d detect no sound.

First, what does it mean to hear a monotonous sound? Is it possible to hear something without difference? No. What we call a continuous “hum” actually contains internal phase differences that change at varying speeds, smoothly or sharply transitioning between one another.

“Continuous” sound inherently consists of changing phases; it can’t be just one state. If there’s no change between phases, it’s indistinguishable. Sound involves a sequence of phases, where at least two phases differ from each other.

What exactly is 1 Hertz mathematically?

A 1 Hz cycle lasts exactly 1000 milliseconds (1 second). It has two distinct peak phases: the top and the bottom points. How many intermediate steps we hear depends on speed.

Below is how one complete phase of 1 second visually looks. Let’s listen to how one hertz sounds in its pure form without looping.

We’ll reproduce a single cycle repeatedly, with brief pauses, preventing the cycle from looping into an infinite signal. Clearly, we hear two alternating sounds: one at the highest point, one at the lowest. Each 1 Hz tone consists of two distinguishable sounds. When increasing frequency, the sounds change, yet remain two short, distinct sounds per cycle.

This beautifully illustrates that even a “monotonous” (single frequency) tone inherently contains at least two distinct phases per cycle. Without these two states, “sound” perception becomes impossible.

What happens when we loop phases continuously at various speeds?

If cycles loop continuously, distinguishing between individual phases becomes more difficult — as if we’re initially looking closely at a single frame (photograph) to catch details, then later seeing it in motion.

How do phases differ from each other externally rather than internally?

Let’s compare what 600 Hz and 700 Hz look like. Clearly, it’s the same “algorithm,” just stretched differently.

In fact, this represents a frequency of phases. It’s as if it’s simply stretched through space. Therefore, it makes sense that the sequence of phases remains uniform and increases according to specific logic or a clear progression. The graph confirms this. Consequently, we can precisely predict the wave shape at any frequency. Length and amplitude scale proportionally.

As we see, everything depends on phase count. Silence in sound means the absence of phase differences. Essentially, sound, at its core, is a single “entity,” principle, or algorithm merely interpreted differently depending on phase changes.

In simple terms:

• Frequency (Hz): how many times per second the wave oscillates, affecting pitch.
• Volume: amplitude — how intensely and how far it propagates through space.

Scientific Evidence of the Phase Law Using Sound as an Example

Sound perfectly illustrates the concept of the Universe’s phase law. Sound waves are nothing more than regular phase oscillations of air pressure, which can be mathematically described and visualized accurately.

What Do Sound Phase Oscillations Look Like Mathematically?

Any sound wave can be described with a simple formula:

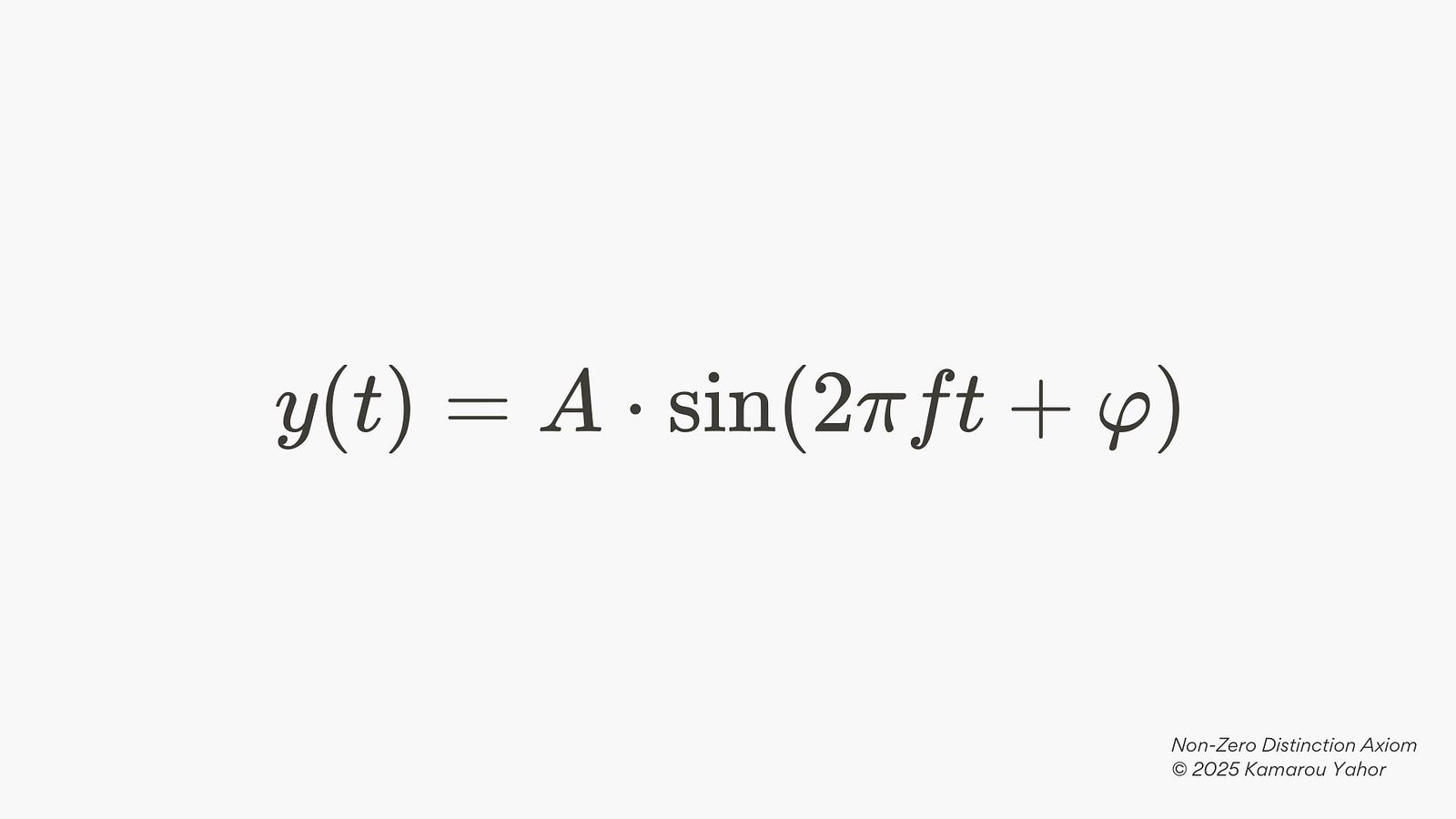
Where:

• A is the amplitude (loudness, the strength of the oscillation).
• f is the frequency (number of phase cycles per second, measured in Hertz).
• t is the duration of time during which we observe the signal.
• φ is the initial phase (the starting point of oscillation).

Practical Experiment and Calculations

Let’s examine five sound frequencies: 100 Hz, 200 Hz, 400 Hz, 800 Hz, and 1600 Hz. According to phase theory, these waves differ only by the number of repeating phase cycles within a unit of time.

In the graph below, you can see waves at the indicated frequencies during a period of 20 milliseconds:

• 100 Hz means exactly 100 complete phase cycles per second.
• 200 Hz means 200 cycles per second, and so forth.

The phase law manifests ideally here: all waves are structurally identical, differing exclusively by the density of phase repetitions over time.

Conclusion from the Experiment:

This experiment demonstrates a direct and rigorous mathematical relationship between frequency (the speed of phase repetitions) and wave shape. Phases aren’t an abstract concept — they’re measurable, observable, and strictly mathematical, underlying sound waves entirely.

Thus, sound serves as direct and experimentally confirmable evidence of the phase law: every change or distinction we perceive in sound is driven solely by phase oscillations. Therefore, the concept of phase theory is absolutely correct and mathematically justified.

Color as Another Form of Phase Activity

Almost everything we see with our eyes follows the same logic of phase differences we saw with sound, only at a different frequency and with different “receiving equipment.” While our ears detect changes in pressure ranging from hundreds to tens of thousands of Hertz, our eyes detect electromagnetic oscillations at frequencies in the range of hundreds of terahertz. However, fundamentally, nothing changes: in both cases, we’re dealing with waves characterized by frequency (k), amplitude (A), and phase (φ).

We don’t see “color” — we distinguish phases of light

Light is an electromagnetic wave.

Our eyes detect oscillations of electric and magnetic fields within the visible range (approximately 430–770 THz). Similar to sound, from the entire spectrum we label certain frequency intervals as “blue” or “red.” But fundamentally, these are just different phases and frequencies, to which our brain attaches labels called “colors.”

Eye as a phase detector:

The retina typically contains three main types of cones (in most people). Each type is sensitive to its specific spectrum (roughly red, green, blue). When electromagnetic waves of different frequencies (k_red, k_green, k_blue) reach the corresponding receptors, three distinct signals arise. Their relative intensity — these three signals (N_obs) — is interpreted by our brain as a “color sensation.”

Color relativity:

What we call “blue” or “violet” isn’t a color stored somewhere in space. It’s a set of wave phases selected by our eyes. Alter the frequency, and the “tone” changes (just as in music). Alter the amplitude, and brightness changes. Everything logically fits into the same phase framework.

LED screens: three waves at different phases

When looking at your phone or computer screen, each pixel typically consists of three tiny LEDs: red, green, and blue. Different intensities of these three waves define the final “color” perceived by your eyes.

Red, green, blue (RGB):

Each diode generates a wave with its characteristic frequency (k_R, k_G, k_B). If only red LED lights up, we perceive “red.” If red and green LEDs shine equally, our brain interprets the combination as “yellow.”

There’s no “yellow wave” emitted:

Our visual system simply combines two wave intervals (two phase ranges) and decides it’s yellow. In reality, there’s an infinite number of possible combinations — displays model them using just three base waves at different amplitudes (intensities).

Intensity equals amplitude:

The higher the amplitude (A_R), the brighter the red subpixel, and the more saturated our brain perceives it. The same applies to blue, green, and their mixtures. This represents another example of “phase difference at step n.”

Exactly like sound, just at a different frequency range

• High frequency (closer to ~700 THz) provides the sensation of “violet,” “blue.”
• Low frequency (just above ~400 THz) perceived as “red,” “orange.”
• Mid-range frequency (~500–580 THz) perceived as “green,” “yellow.”

Similar to audio:

• Higher frequency (k) = closer to violet (like high notes).
• Lower frequency (k) = more red (like lower notes).
• Loudness corresponds to wave amplitude (brightness).
• “Timbre” is the combination of various frequency components (complex spectra — mixtures of red, green, blue, etc.).

Thus, color is not an object property, but a phase property

When we look at a rainbow, it seems nature drew colored bands in the sky. But these bands are merely different phases of the white-light spectrum separated by raindrops into distinct frequencies. The brain reacts differently to each band, assigning each one its own color.

• Eyes receive different k values.
• Neurons signal “red/blue/green.”
• The brain “paints” a color that exists nowhere except our consciousness.

Just as in music: the notes “C” or “A” don’t inherently exist. There’s a wave at 440 Hz, and ears recognize “Oh, that’s an A note!” Phase differences create tones, while our perception labels them as “color” or “sound.”

Thus, color is just another illusion of phases. When you see something “red,” your eyes are merely responding to electromagnetic oscillations (E/M waves) at specific frequencies, and your brain attaches a “red” label. Outside our perception, the concept of “color” does not exist; there are only wave phases and energy.

Thermal Imaging as an Alternative to Human Vision

Thermal imagers (infrared cameras) are devices that detect radiation in the infrared (IR) range. Physically, these are the same electromagnetic waves as visible light but with longer wavelengths, lower frequencies (k), and consequently, lower photon energy.

How a Thermal Imager Works

Any object with temperature (T) constantly emits electromagnetic radiation (Planck’s law: higher T means greater emission and shorter wavelength).

Infrared optics (such as a germanium lens) transmit long-wave radiation, focusing it onto a sensor array (similar to the photosensitive array in an ordinary camera, but tuned specifically to IR).

The sensor array detects IR-wave intensity (the number of “phase ticks” within this range). Each pixel outputs a signal proportional to local brightness around (k_IR).

The processor translates this into “pseudo-color”: brighter pixel emissions appear as “hotter” colors on the screen.

The Same Phase Principle

Human eye visible range: approximately 4×1⁰¹⁴ — 8×1⁰¹⁴ Hz (violet → red).

Thermal IR imaging range: approximately 1⁰¹² — 1⁰¹⁴ Hz (longer wavelength → lower frequency).

The fundamental principle doesn’t change; it’s the same sine wave, scaled differently by k.

We call it “hot” or “cold” because the brain translates it into colors (orange, violet, green) through internal algorithms. But objectively, it remains merely a different phase of electromagnetic waves.

Why Thermal Imagers “See” What We Can’t

Human eyes are tuned to a relatively narrow frequency band (k), corresponding to visible light. Infrared waves are beyond the “red” side of the spectrum, making them invisible to our eyes.

Thermal imagers extend our phase-detection capability, capturing lower-frequency waves where objects around ~20–40 °C emit most actively.

Thus, thermal imaging serves as yet another illustration of the phase principle:

We simply “shift” the detection range (k) of the sensor.

We capture frequency components missed by our eyes.

We portray them as pseudo-color images; fundamentally, they’re just the same “phase distinctions,” only in the infrared range.

The Phase Mechanics of the Universe in One Simple Line

The example of sound clearly demonstrates that time or distance are merely measurement methods, relative and not affecting the basic form of a wave or its phase sequence. Underlying every wave is one fundamental shape: a sine wave. The only difference between waves is the number of repetitions of this basic form. These repetitions create phase differences.

Allow me to show you the profound meaning of this simple law through a single line of symbols, without complicated math or formulas:

I II III IIII IIIII IIIIII IIIIIII IIIIIIII IIIIIIIII X

• “I” is the original unified form (phase).
• “II,” “III,” “IIII,” and so forth represent repetitions of the form, increasing by one additional repetition at each step.
• “X” symbolizes a completed cycle (the combination of phases from 1 to 9, returning to the original state), analogous to the numeric cycle from 1 to 9 and returning to 0.

Thus, “X” represents a point of phase resonance — the completion of a cycle and the beginning of a new repetition. Mathematics demonstrates this through the digit “0,” a closed loop symbolizing the infinite repetition of cycles.

Moreover, this simple line hides another rule — the pattern of spacing between symbols (phases):

Try mentally inverting spaces and symbols to see precisely how distances between them change.

You’ll notice intervals between phases follow a strict, clear, and immutable law of increment. This is the key to understanding phase cycles of the Universe.

This simple sequence visually demonstrates the fundamental law of the phase mechanics of our world:

A unified form → repetition → accumulation of differences → resonance → completion of a cycle and the start of a new one.

Now it becomes clear how Roman numerals were intuitively invented. Nature itself seemingly provided an easy and natural guideline. The creation of mathematics became inevitable since it directly reflects the phase mechanics of the Universe.

The Most Astonishing Experiment with Animation

I wondered, what if we create a sequential phase animation, similar to amplitude modulation, where speed incrementally increases and decreases? Here’s what resulted:

Observe the animation formed by squares that are entirely unrelated to each other. They merely move vertically at different speeds, sequentially arranged by speed increments. Watching the animation, you’ll notice it visually depicts sound waves at varying dynamics.

But most intriguingly, if I compile all phases into a single static image, it results in one indistinguishable picture. Regardless of the playback speed of the animation, their phase pattern remains constant, repeating identically and becoming indistinguishable. Pay close attention to the timeline below.

The key: A single operation — “add another tick of the same shape,” combined with small tempo differences → produces a predictable cycle: wave → chaos → synchrony → wave.

I’ve demonstrated visually what we call dispersion and beating rhythms in sound, Laplace resonances in astronomy, and baryon oscillations in cosmology. It’s the same law of phase progression — only differing in scale and energy.

Indeed, the “nature of the Universe” looks exactly like this, only with significantly more cells, and frequencies ranging from femtoseconds (photons) to billions of years (large-scale cosmic foam). This animation provides a compact visual proof-of-concept of phase theory.

Thus, when we reduce something to indistinguishability, we perceive the true property of matter; otherwise, matter exists merely in repetitive phases if considering simple linearity.

For a long time, I couldn’t understand why water becomes a structured lattice when freezing, rather than freezing into static chaos — then I realized:

Gas, liquid, ice — they aren’t different substances. They represent different distances and ways molecules vibrate relative to each other. When temperature reduces these distances, we see the crystal lattice structure and cyclicity of the substance. Ice, water, and steam differ solely by intermolecular distances:

• Gas (vapor): H₂O molecules are distant, nearly non-interactive, moving rapidly.
• Liquid (water): Molecules moderately distant, interact weakly, fluidly.
• Solid (ice): Molecules very close, arranged in crystalline lattices, barely moving.

All substances follow the same “script” of phase transitions; otherwise, the formation of ordered lattices would be impossible.

Scale Invariance

At our level of perception, when we freeze water, we observe indistinguishability — a static cube of ice. At the molecular level, we find a similarly stable indistinguishability in the form of a crystalline lattice. Yet the internal phase properties of the object aren’t lost. These properties are scale-invariant, cycling continuously at different scales of perception. If we zoom down to the atomic level within the lattice itself, the exact same sequence repeats, similar to what we observed with sound.

It’s the same distinguishable structure, embedded within itself at every scale level. The unique aspect of the entire molecular world is that substances interacting at various tempos of active phases generate a vast number of combinations. There’s a certain level of “noise,” or deviation, everywhere, and these substances influence each other. Without this noise, we would revert to the problem of indistinguishability once again.

This is precisely why we can pour liquids of different phase activities into a glass, and they will arrange themselves into the same recursive sequence. At the bottom of the glass, substances will settle relative to each other according to low phase activity, with those of higher activity settling above.

Science calls this density, but this is a phase activity relative to each other.

Energy in Sound (Loudness)

It logically follows that the more oscillation phases created, the greater the energy needed for what we call “sound.” This is precisely why higher frequencies require significantly more energy to be heard over distances — they expend their energy faster while traveling through space. That’s why, from far away, music typically reaches us as a muffled rumble of low bass notes, or why we mostly hear bass coming through walls.

And what about loudness, you ask? Loudness is simply the amount of force applied to move “molecules,” which in turn push other molecules. These molecules then vibrate our auditory apparatus at varying rhythms, and our brain subsequently interprets and recognizes these vibrations. Thus, music — despite its seemingly simple arrangement of sound waves, essentially transmitting a sequence like “01010101010101” at varying intervals — is genuine magic.

Incidentally, in a vacuum, there’s no sound because there are no molecules to vibrate.

Conclusion:

1. Phases follow a clear sequential law (geometric progression).
2. Sound represents phases of “space” oscillation at varying intensities — if there’s no oscillation, there’s no sound.
3. The more dynamic (frequent) the phase, the “higher” the pitch — but this requires more energy for the sound to travel farther.

If a tree falls in a forest and nobody hears it, does it still produce a sound?

Yes, absolutely — physically, the tree generates sound waves when it falls. The oscillations of air occur regardless of whether there’s an ear nearby to perceive them.

The Brain Expends Energy on Frequency Processing of Movement Differences

The visual system (retina → optic nerve → visual cortex) processes incoming streams of photons, extracting motion, contours, colors, and so forth. When viewing more complex scenes (many flickering objects, high-frequency changes), the brain indeed expends greater resources for analysis.

Fatigue:

When we are fatigued (energy deficit, decreased neurotransmitter levels), the brain finds it harder to perform rapid and detailed processing. As a result, we may “miss” quick details and struggle to notice small or rapid changes.

Does Looking More Mean Using More Energy?

The brain consumes approximately 20% of the body’s total energy at rest. Research on brain metabolism (Sokoloff, 1977; Raichle & Gusnard, 2002) indicates that even at rest, the visual cortex remains one of the most active areas.

Source: Raichle & Gusnard (2002) — “Appraising the brain’s energy budget.”

Visual Processing Requires Energy:

fMRI and PET scan studies confirm that processing moving images (compared to static ones) activates the occipital lobe more intensely.

Source: Tootell et al. (1995) — “Visual motion aftereffect in human cortical area MT.”

The Impact of Frame Rate (FPS) on the Brain

High FPS and Cognitive Load:

In gaming and virtual reality, frame rates above 60 Hz reduce latency and increase fluidity, but demand more neural processing:

Research: Lambrechts et al. (2013) — “The impact of frame rate on user experience in games.”

Conclusion: At 120+ Hz, the brain processes motion more quickly, but fatigue can set in sooner due to increased visual cortex activity.

Energy Expenditure and Fatigue

A high FPS, especially in dynamic scenes, increases the load on the visual system:

Research: Kennedy et al. (2010) — “Visual fatigue and spatial frequency adaptation.”

The more frequently images change, the greater the workload for neurons, thus requiring more ATP (energy).

All of this once again underscores the inseparable link between time and energy.

Why Does the Universe Employ Different Frequencies of Perception?

Frequency is the “language” of matter.

Imagine an orchestra: you have string instruments (violins, violas, cellos), wind instruments (flutes, oboes, trumpets), and percussion instruments (timpani, drums).

Each instrument (and musical part) can play in its own rhythm or tempo, even though they all align with a common musical “meter.” For instance, violins often perform fast melodic passages (16th notes), while double basses move in slower rhythms (quarter notes), and timpani strike accents even less frequently.

What if all instruments were strictly tied to a single, uniform rhythm (let’s say only even quarter notes), without the ability to accelerate or slow down? You’d end up with a monotonous soundtrack — no polyphony, no diversity. All music would sound “single-layered,” devoid of intricate transitions or harmonies.

Why do we need different frequencies in music?

Because it creates complexity, a combination of different voices (faster-slower), and harmonic diversity. This complexity gives beauty and structure to orchestral performances.

Physics analogy:

Nature, similar to an orchestra, has different processes operating at different speeds (or “frequencies”). Some happen in nanoseconds (molecular oscillations), others in seconds (biochemical reactions), and yet others take thousands of years (geological evolution).

If all processes (throughout the entire Universe) were forced into a single rhythm (“one frequency of time”), we would never witness complex levels of organization; everything would oscillate (or move) in perfect synchrony.

Synchronization:

Prevents quarks, cells, and stars from directly “communicating,” as this would be energetically inefficient.

Complexity:

A hierarchy of frequencies allows the creation of multi-level structures (atoms → molecules → organisms → galaxies).

Observability:

If everything operated at 1⁰²⁰ Hz, we’d perceive only noise. If at 0.001 Hz, we’d never notice our own existence.

Frequencies are like gears in the Universe’s clock: small ones rotate quickly, larger ones slowly, but together they indicate what we simplistically call ‘time’ — though it’s merely an agreed-upon rhythm coordinated among all components.

(This model explains why we don’t observe quantum effects in everyday life — our “detectors” are tuned differently.)

Why is this beneficial?

Protection from overload:
If we perceived all phases, our brains would explode from data overload. Or it would simply require significantly more energy to process all information in time.

Stability of reality:
Indistinguishability of ultra-fast phases creates an illusion of continuity.

Connection to dark matter:

Its “invisibility” might be a result of phase mismatch (>1⁰²⁸ Hz).

Indistinguishable phases aren’t a bug; they’re a feature of the Universe. They ensure reality remains stable for observers at our perceptual level.

So What Exactly Is a Clock?

Prepare yourself — because after this, you’ll never look at clocks the same way again, especially if you’ve never delved into physics deeply.

Here’s a short and very straightforward explanation of what clocks truly are:

Clocks are essentially precise scientific instruments.

Measurement devices: Thanks to clearly marked increments (seconds, minutes, hours), we can accurately and without confusion say how many “beats” have passed from the beginning to the end of any event.

Synchronization: Clocks allow us to synchronize phases with other people. For example, if we use the “hour” as a beat within a 24-phase cycle (one day), we might say, “Let’s meet at 17:00.” But if we lived on another planet with a different day-night cycle, we’d need different clocks — for instance, Martian clocks.

Predicting phases: Additionally, clearly marking which phase corresponds to the cycle lets us look at clock hands (or digital numbers) and instantly understand how many phases remain until another desired phase (such as sleep, awakening, meetings, etc.).

Clocks Are Local Decoders of Planetary Beats

On Mars, a day lasts about 24 hours and 39 minutes (Earth time). If we lived there, using “24-hour” Earth clocks would be inconvenient. The Martian “day” and “night” would constantly shift relative to our Earth-based measurement. It becomes obvious that another planet, with a different rotation period, would require different clocks.

NASA has already encountered this issue when working with Mars rovers. They introduced the term “sol” as a separate unit for Martian days (~24.6 Earth hours). Thus, “07:00 sol” would mean morning “on Mars,” though on Earth it could correspond roughly to 07:39.

However, following my theory of time, we could simply say: “The cyclical beat of Mars, relative to day and night, is 24.6 hours,” without introducing terms like “sol.”

This example clearly demonstrates that absolute time doesn’t exist. We simply adjust “clocks” to match local cycles, dispelling the illusion that “24 hours” is some universal cosmic standard.

The “Future” as a Controlled Change of Phases

Here, I’m describing a more philosophical view of “time travel,” understood as adjusting the speed of phase transitions.

When we grasp phase dependencies and sequences, it becomes clear that to truly travel through phases of differences (time travel in the classical sense), one would need to rewind the entire Universe backward, returning every atom to its original state. You couldn’t alter anything in previous phases without instantly destroying all subsequent ones.

But what if we instead viewed this as changing the speed at which phases occur? An object (or a person) can determine how rapidly it transitions through phases — moving from point A to point B in the Universe’s coordinate system — by expending more or less energy.

A simple example:

Someone decides to walk (slow energy consumption — slow transition to the “future”) or drive a car (fast fuel consumption — faster coordinate shift).

So, when we say we’re “waiting for changes,” we’re essentially waiting for the Universe’s phases to reach a certain desired point of difference. However, we generally don’t precisely define it. Because to define and manage one’s future, one can only adjust their phases within the limits of sequential transitions. This concept is highly simplified, of course, as we remain strongly interconnected and dependent upon each other, all forming one unified phase picture of the Universe. Moreover, if all phases are deterministic, sequential, and interdependent, then our sense of choosing the pace and sequence of these phases is merely an illusion. But that’s a topic for another article.

The “Future” of Other Objects

At the same time, it’s impossible to “jump” immediately to a distant point in time, bypassing phase sequences. Every system changes its coordinates and internal states sequentially, step by step.

We can only accelerate or slow down this evolution, but never “skip” intermediate stages.

The Universe Is Indifferent to Our Speed

From the standpoint of global processes, it doesn’t matter whether an object moves very fast or extremely slowly — the Universe records all phases (every atomic change).

This means there are no “cheat codes” allowing one to skip ahead without passing through the sequential steps. We can merely stretch or compress the intervals between these steps.

Conclusion:

The idea of the “future as a controlled change of phases” clearly emphasizes that we are free to expend energy to accelerate events within our own local “space.” However, the Universe as a whole continues its global development along its predetermined sequence.

We don’t “jump” to the future (a desired phase); rather, we manage the speed at which we reach it — but only within the limits of our available energy and external constraints.

Non‑Zero Distinction Axiom

N ≠ 0 — the Reference Point of Reality. The Entire Universe Starts from N ≠ 0.

This concise formula expresses the “Axiom of Distinguishability”: the Universe becomes observable precisely at the moment when at least one distinguishable beat, event, or phase click emerges. As long as N — the number of such distinguishable acts — is equal to zero, neither space, nor time, nor measurable quantities exist. A non-zero N generates everything else: seconds and meters, temperature and energy, even the very fact of an observer’s existence.

This illustration underscores a crucial insight: all physics, logic, and computation begin from the simple condition N ≠ 0.

Logical Zero

If N = 0, no state can be distinguished from another; thus, observation, measurement, and even the concept of “existence” itself become impossible.

Ontological Starting Point

N ≠ 0 establishes the fact of the first difference — the first “non-nothingness” point — from which the empirical Universe emerges: matter, spacetime, and all the laws of dynamics.

Universality of “N ≠ 0”

• In biology, the first counter of difference divides the cell cycle into phases G1, S, G2, M: life begins when rest transitions into synthesis.
• In computer science, the same principle reduces to the 0/1 bit — the minimal switch on which all computation relies.
• In physics, the quantum state “excited — non-excited” defines an atom’s spectrum, generated by a single phase shift.
• Even religion relies upon this principle: In the Book of Genesis, the first creative act was distinguishing between the solid earth and the expansive sky. Quotation: “In the beginning God created the heaven and the earth.” (Genesis 1:1)

Consciousness also emerges from a non-zero difference

We become conscious precisely because we distinguish the “I” from the “not-I.” We understand we are not a tree, not a river, not the sky, not the sun — indeed, none of what surrounds us. And it is precisely phase differentiation that enables this act.

Thus, N ≠ 0 is not merely a formula; it is a fundamentally necessary philosophical and scientific act of existence — the very first boundary separating reality from nonexistence.

• N_obs — the number of “clicks” (distinguishable phase transitions) that occurred in the observed process within a chosen observation window.
• N_ref — the number of clicks occurring in the reference (standard) accepted as the measurement unit.
• Q — the measured quantity itself. It is simply the ratio of these counters, and thus dimensionless until we assign a label (“second,” “meter,” “degree”).
• δ — the relative error (random fluctuations, environmental noise, instability of the standard).
• δ_crit — the critical threshold of distinguishability for an instrument or observer.

If the absolute value of δ is less than δ_crit, the quantity is considered “the same”; if greater, we record that the system has transitioned into a new phase.

The Meaning:

We compare how many phase-clicks the observed object made against how many the reference made. While the relative deviation remains within an acceptable threshold, we say the object remains in the same phase (“the same temperature,” “the same second”).

However, as soon as the proportion of deviation surpasses the critical mark, the counters no longer compensate each other, and a new observable-distinguishable state emerges.

Thus, the formula integrates:

• A pure ratio of events (N_obs / N_ref) — the fundamental basis of any physical quantity.
• Acceptable error (1 ± δ) — the actual sensitivity of an instrument.
• A criterion for determining whether a phase is “equal” or “no longer equal” (threshold δ_crit).

This mechanism is precisely how “seconds” are separated from each other, “meters” don’t become kilometers unintentionally, and ice becomes distinguishable from water. The difference is registered exactly at the point where the relative counting error first exceeds the critical threshold.

That’s all: a single progression plus one allowance for fluctuation. If you want to call this “time,” “temperature,” or “pressure,” just divide, measure, and assign your units — the mathematics won’t object. But the fundamental logic remains unchanged: every phenomenon is the repetition of a recognizable form until the energy (step size) and noise (vibration) surpass the critical ratio. Everything else is just notation.

For the basic, meta-level task, this is indeed the “best” (shortest yet fully complete) formula. Everything else is an extension tailored to specific disciplines.

Repetition (Structure)

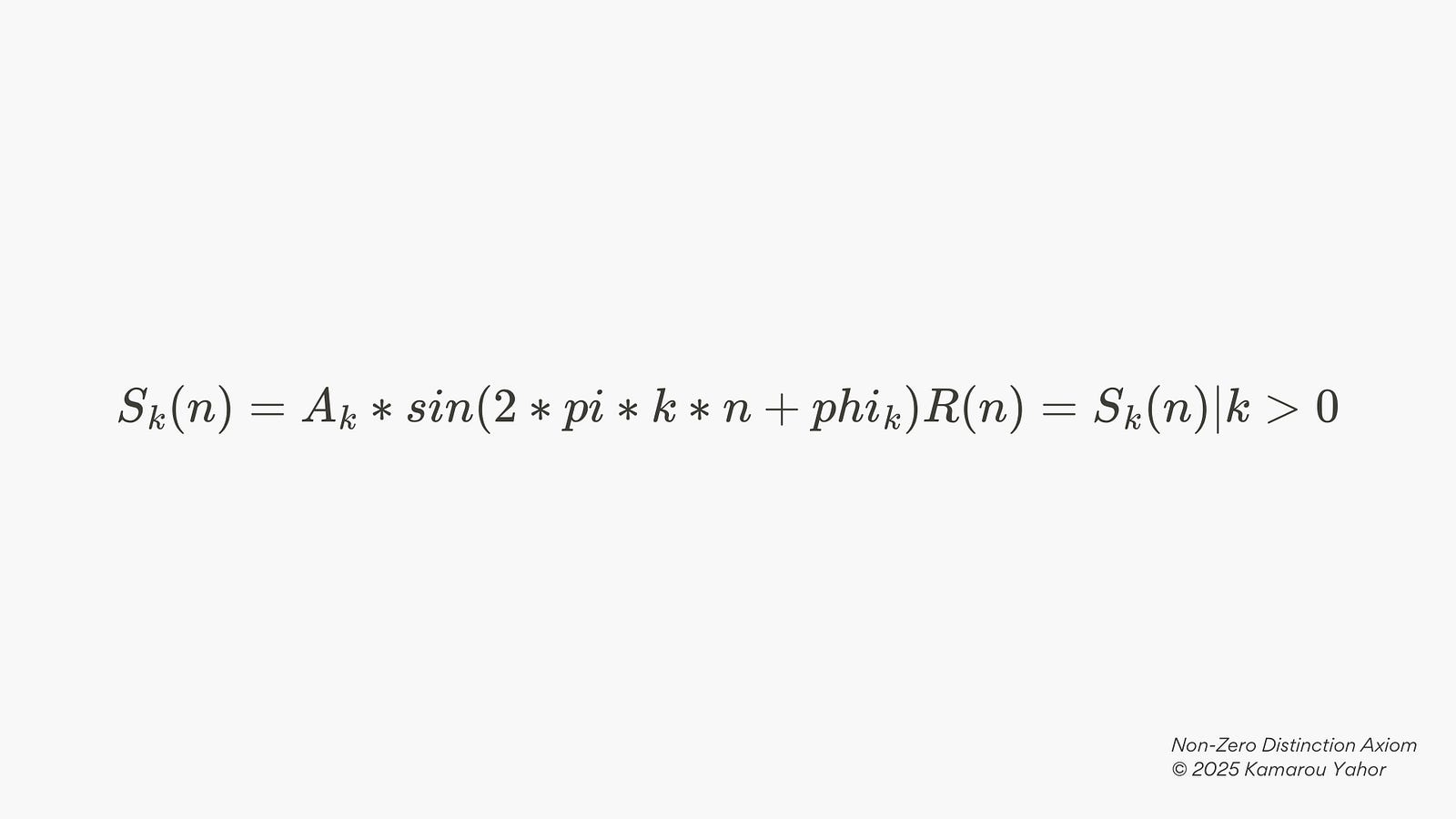
The formula demonstrates that any phenomenon can be represented as the same basic sine function, played back at different speeds (k). All reality is simply a collection of these phase copies, with scale and resonance determined only by the coefficients of these copies.

1. Repetition: One pattern — infinitely many copies

Any observable phenomenon can be considered a repetition of the same fundamental shape (sin()), simply cycling at different speeds (k):

• Sound: oscillations in air pressure; the same sine, but in a range from hundreds to tens of thousands of Hertz.
• Light: an electromagnetic wave; the same shape but with a vastly higher frequency (k).
• Crystals: spatial sine; lattice nodes repeating at angstrom-scale intervals.
• Planetary orbits: elliptical motif repeated with multiples of orbital periods.
• History, fashion, market cycles: sociocultural rhythms — “the new is the well-forgotten old.”
• Biological rhythms: breathing, pulse, sleep/wake cycles, age-related phases.

2. Balance: Resonance as a pivot node

In any system where there is movement, we observe:

• A growth phase,
• A declining phase,
• A transitional point (resonance) — the moment when two oscillations become multiples of each other (k₁/k₂ = p/q).

It is precisely this node that shapes the cycle: the pendulum reverses direction, the string reaches maximum volume, and an economy transitions from growth into recession.

3. Scale: the same geometry across all levels

Multiply the argument n by any coefficient λ, and you get the same sine wave on a new scale:

• Fractals: from cabbage cross-sections to coastlines, we observe self-similarity.
• Music: every octave doubles the frequency (k); modulations and variations are shifts of the fundamental beat.
• Color spectrum: a continuous scale rather than discrete “color points.”

The world is defined not by absolutes but by the relation of phases. A galaxy and a qubit follow the same “phase carousel”:

• The pattern remains constant,
• The frequency of ticks increases from macro-world to quantum level,
• Noise (σ) either performs useful work (if σ is below threshold τ) or blurs the structure (if it exceeds control limits).

A turbine, an atom, and a qubit are all governed by the same law of distinguishability; the difference is only how many cycles we can “capture” per second and how costly it is to keep noise below the critical level. Hence, the interest in quantum technologies.

No exceptions.

• Deterministic chaos: hidden phase rules of strange attractors.
• Quantum mechanics: still the same phase interference; “randomness” appears only because we register the squared amplitude and lose track of the phase itself.

In other words, quantum “noise” isn’t nature’s secret roulette wheel, but rather a hidden difference in phase angles concealed beneath measurements.

Thus, every phenomenon — whether sound, orbit, DNA exchange, or stock market fluctuations — is fundamentally the same basic oscillation, differing only by its speed multiplier, resonance node, and observational scale.

Calculating Lifespan Through Phase Changes

The phase-based approach shifts us from the abstract concept of “lifetime” towards a concrete, measurable count of phase changes. The lifespan of any resource — be it a battery, a device button, or a human organ — can be clearly and simply described through this fundamental formula:

Where:

• Tlife: The lifespan or resource duration of an object.
• Ntotal: The total number of available phase transitions.
• f: The frequency of phase transitions (how many transitions occur per unit of time or action).

This formula is fundamental because it highlights a core principle: the lifespan or durability of any object isn’t abstract — it is directly measurable by counting phase transitions.

Why This Matters:

It’s Universal:

• Batteries: Measured in charge-discharge cycles, not years.
• Human Heart: Lifespan correlates with total heartbeats (~1–1.5 billion beats for mammals).
• SSDs: Endurance is rated in write cycles, not calendar time.

It’s Measurable:

• Apple tests iPhone buttons for 100,000 presses.
• Car tires are rated in miles/km (rotational cycles).

It’s Physics, Not Philosophy:

Every phase change consumes energy and increases entropy. Faster transitions (higher frequency f) consume available phases (Ntotal) quicker.

Clear Examples:

• Hummingbird vs. Whale:
• A hummingbird’s rapid heart rate (high f) leads to fewer total beats (Ntotal), resulting in a shorter life (Tlife). Whales, with slower heart rates, live significantly longer.
• Engine Wear:
• Higher RPM (f) accelerates engine wear (Ntotal), reducing durability.

Limitations and Precision:

• Nonlinear Effects: Temperature, corrosion, and regeneration mechanisms (e.g., cellular repair) can alter the total available phases (Ntotal).
• Interpretation Flexibility: The frequency (f) can represent any stressor — heat, pressure, voltage — if it is tied to measurable phase changes.

The Big Idea:

“Lifespan isn’t about time — it’s about how many times a system can change before it wears out.”

Practical Examples of Phase-Based Approach:

• Power banks: Number of charge-discharge cycles.
• Car tires: Number of rotations or kilometers driven.
• Light bulbs: Number of on-off cycles.
• The human heart: Number of heartbeats, rather than abstract years of life.

The phase-based approach clearly demonstrates that an object’s lifespan or durability is defined not by abstract time, but by concrete, measurable phase changes. This is not philosophy — it’s a fundamental physical law of distinguishability applicable to everything around us.

Fundamental Principle (Key Insight):

Every phase change has its price. This cost can vary dramatically. Even when nothing appears to change, distances between molecules still gradually increase — these too are phase changes. The universe obeys this law of distinguishability and decay. Nothing remains unchanged; everything inexorably moves toward dispersion and disorder.

Energy: From the Big Bang to Inevitable Decay

The phase law states that any phase difference requires initial energy. The entire Universe as we know it today — planets, stars, galaxies — exists due to one single initial impulse of energy. In this context, the Big Bang theory is close to the truth, although its interpretation is often incorrect.

We are not endlessly accelerating, expanding the Universe — we are gradually decaying.

Imagine a car standing still on a road. Its speed is 0 kilometers per hour. When pressing the accelerator pedal, we don’t “create” energy. On the contrary, we begin to expend it, consuming fuel. Similarly, the entire Universe, set in motion after the Big Bang, doesn’t accelerate by itself — it inevitably loses energy, gradually slowing down its phase cycles and fading out.

Everything we observe today isn’t an endless acceleration, but a gradual expenditure of that single impulse provided at the beginning. Stars burn, planets rotate, galaxies move, all slowly losing energy. Each passing second takes us slightly further away from the original source.

This means that the natural direction of the Universe isn’t infinite expansion, but inevitable decay. If we wish to exist longer, if we want to live and evolve, we must move against this current. We must seek energy not away from the source, but toward it — back toward the original phase impulse.

A Truth We Cannot Turn Away From

Reality is simple and relentless: our planet is gradually slowing down its rotation. Each day becomes longer by approximately 1.7 milliseconds every century. This fact is confirmed by precise astronomical measurements. Today, this may seem insignificant, but over millions of years, it will accumulate into a noticeable difference. Ultimately, Earth — like every other object — gradually loses energy, slowing its rotation around its axis.

From the viewpoint of a human lifespan, this might seem eternal — billions of years. But the Universe offers no guarantees. No one can be certain that somewhere behind us, an object with greater energy and speed hasn’t emerged, racing directly toward our Solar System. No one can exclude the possibility of a collision with a cosmic body born from chaotic processes occurring every second. Space is unpredictable, and internal interactions can instantly alter all plans.

The Best Example is a Glass of Water

Imagine pouring a glass of water from a great height on a hot day. What will happen?

The water breaks apart into hundreds of droplets of different sizes. Large and small, heavy and light — each drop has its own speed and fate. Some drops merge, becoming larger and heavier. Others break apart into tiny sprays, instantly evaporating beneath the scorching sun, never even reaching Earth’s surface.

This is exactly what the Universe is like.

Every galaxy, every star, and every planet are like drops of water falling from the sky. They possess varying amounts of energy, differing trajectories, and lifespans. They can merge, consuming each other, or split apart and vanish sooner than we imagine. At any moment, their fate may change due to the slightest internal or external interaction, random collision, or sudden burst of energy.

We, humans, live on one such droplet. And we’re not guaranteed eternity.

Our only chance is to move consciously, understanding the law of distinguishability and phase cycles, seeking energy not in expansion or infinity, but where it becomes greater — closer to the beginning, the origin of all motion.

Energy is not something we create now; it’s something we once received and must preserve. The only way to prolong the existence of any process is to move against entropy, against natural decay, back toward the source of distinguishability — to the very first point where it all began.

Precisely there, against the current, we can continually rediscover energy anew.

Simplified Universe Simulation Based on Phase Theory

To vividly illustrate the principles of phase theory, I created a simplified simulation of the universe based on an intuitive yet elegant mechanism of phase changes.

Simulation Overview:

Starting Point: Particles (represented by squares) emerge from a common origin, each with unique characteristics.

Phase Differences and Energy:

• Particles with greater mass (lower frequency of phase changes) move more slowly but retain their energy longer, traveling further.
• Particles with lower mass (higher frequency of phase changes) move faster but quickly exhaust their energy and fade.

Cyclical Process of Decay and Potential Renewal:

• Particles travel until they reach the opposite edge of the simulation field. Upon reaching this boundary, particles with the greatest mass lose their phase energy and start to decay.
• After decay, particles theoretically return to the origin at the speed of light, potentially forming new matter again, thus repeating the cycle. This cyclical process resembles Earth’s natural water cycle, where matter continuously transitions between states of order and chaos, possibly cycling back into order again.

What Does This Demonstrate?

This model clearly illustrates a fundamental principle of phase theory: every phenomenon in the universe — from elementary particles to complex structures — is governed by phase changes, inevitably leading to decay and possibly renewal.

I cannot assert this with absolute certainty, but logic strongly suggests that processes within the universe are cyclical rather than linear. In a long-term perspective, the universe may maintain balance through continuous cycles of decay and renewal, shaping what we perceive as reality. Just as Earth exhibits closed-loop systems in nature, the universe itself might utilize similar cyclic mechanisms universally.

Nothing truly disappears; instead, everything transforms. Phase and energy are interconnected: the faster the phase changes, the shorter the lifespan of any given object or system.

Connection to the Big Bang and the Universe’s Shape

The theory and formula I’ve employed in the animation visually reflect the concept of the Big Bang, much like the renowned illustration by Pablo Carlos Budassi, “A logarithmic scale captures the whole universe”

In a sense, the universe can be compared to a candle flame. I’m not convinced that the universe is infinite, as infinity contradicts the fundamental law of decay governing all things. More likely, our universe possesses a closed geometric form, potentially structured by amplitude patterns or perhaps something even more fascinating and intricate. However, these remain reflections and theoretical considerations for now.

Manifesto of Distinguishability

Everything we once knew about the world began with the illusion of absolutes. We believed time flows by itself, that seconds or meters exist independently of measurement, that temperature is something absolute, given to us once and for all.

Today, I seek to open your eyes to a new truth.

There are no isolated seconds, meters, or kelvins. There is no absolute time or space. No object, phenomenon, or event exists by itself. There are only phases and differences between them.

The world does not begin with the Big Bang — it begins with a simple condition of distinguishability, with a non-zero counter of phase transitions. It begins with a simple universal law stating that nothing can remain at zero; everything must move, without exception. Therefore, the decay of everything is inevitable. If N = 0, there is no reality — no observer, no observed. But once the first non-zero difference emerges, it sets in motion an endless chain of consequences, which we call life, matter, energy, and time.

What does this mean practically?

It means that every atom, every cell of your body, every bit of information, every second of your life is not an independent entity, but rather a phase counter you have chosen to use. Every measurement you make is simply a ratio of two numbers, two clicks, two beats. The world isn’t absolute — it is relative, phased, proportional.

From this arises the most crucial idea:

Distinguishability is primary. All reality emerges and exists through it. Distinguishability is more fundamental than energy, deeper than matter, more real than time and space. Physics, biology, chemistry, computer science, even religion and art — they are merely different ways of counting phases.

What now?

Now, we must reconsider all scientific disciplines. We must develop measurement instruments that directly operate with phases, bypassing the conventions of outdated units. We must view chaos and randomness not as anomalies, but as manifestations of phase regularities still invisible to us.

And most importantly:

We now understand that the Universe isn’t somewhere “out there” — it’s right here, within us, in each act of distinguishing.

When you open your eyes, when you hear a sound, when you sense warmth or cold — you create the world anew through a simple act of phase distinction.

This is the most fundamental discovery:

Reality begins with you. With your capacity to distinguish. The entire world is a single phase dance. And you are not merely an observer — you are the source of reality.

You are the origin of distinguishability.

How does your model describe quantum uncertainty?

You might ask me: “How does your model describe quantum uncertainty? Interference, decay, tunneling?”

And I will ask you in return:

Can you record phase changes occurring at the ultimate speed of light?

No. Because you have not yet built a device capable of distinguishing phases that shift faster than your equipment can capture.

And if you cannot capture these phases, you cannot say whether true randomness exists there — or simply an indistinguishable regularity. If something is indistinguishable, it is indefinable. If indefinable, it is not objective. If not objective, it falls outside the bounds of scientific judgment.

Thus, it’s not you who has the right to ask how my model explains “uncertainty” — rather, I have the right to state that quantum uncertainty is merely the threshold of your technological distinguishability.

Build an instrument that can detect phases at the speed of light, and then we’ll talk. For now, my model explains more than yours: It accounts for what is visible and also what remains hidden due to phase indistinguishability.

Article Supplement: A Response to Skeptics and the Theory’s Status

To critics and researchers: I understand your interest and your questions. And I want to emphasize:

My theory is not an argument against physics but a reformulation of it.

It does not negate established laws; rather, it shows that all measurements occur within a more fundamental phenomenon — phase distinguishability.

Many of you demand “proof” — numbers, formulas, experiments. That’s understandable. But one point is crucial: I don’t claim to explain “how”; I answer “why.”

Important to understand:

1. This is not a theory requiring overly complex calculations.

It is a new way of thinking that you can apply yourself.

Take any phenomenon and reconsider it — not through seconds and meters — but through phases (N) and their ratios (Q = N_obs / N_ref).

2. This is not competition with physics.

Physics explains mechanisms. I propose a frame of reference where these mechanisms become understandable at the level of the very origin of fundamental categories — time, energy, measurement.

3. This does not require faith.

It requires observation. You can test this model with any process — from a pulse or a pendulum’s swing to photons and cellular respiration.

Wherever there’s distinction — there’s a phase. Where there’s a phase — there’s counting. Where there’s counting — there’s physics.

Examples of questions you can reconsider phase-wise:

• Why do atomic clocks exhibit different errors under identical conditions?
• Why is biological aging nonlinear?
• Why does the same laser affect substances differently at varying temperatures?

The answer is already within the model: You count seconds — but you should count phases. The second is derivative. The phase is primary.

Why this is a foundation rather than an equation:

Calculations are tools. I provide an alphabet from which any formulas can be constructed.

This is axiomatic:

• N = 0 ⇒ no observable world
• N ≠ 0 ⇒ a distinction arises, and with it — everything: time, energy, matter

This isn’t about “replacing formulas.” It’s the language in which formulas are written, if you understand their deeper meaning.

You can critique something that fits into your paradigm. My model is a new paradigm. Either you accept it as a starting point and seek conceptual inconsistencies within it, or you continue measuring phases with seconds — and then your skepticism simply exists within the wrong coordinate system.

I’m not asking for recognition. I am offering a tool. A foundation isn’t proven. It’s built upon.

Now — the next move is yours.

Conclusion

My approach clearly demonstrates the relational perspective on time, showing that “time” is not some magical entity but a specific definition. Simply put, I would describe it as the length of intervals between phases of difference among objects in space. It is precisely these intervals that allow us to observe the diverse phase frequencies of the world.

Note

All numerical values presented serve as reference points, illustrating the easily traceable pattern “phase ↔ scale ↔ resonance.” I intentionally avoided presenting every number to the last significant digit, as real-world phenomena are subject to fluctuation noise: an infinite interplay of interactions slightly shifts frequencies, amplitudes, and timestamps, disrupts ideal symmetry, and introduces randomness. Yet, even through these variations, the same basic law of distinguishability emerges, and the allowance for noise error (± δ) in formula Q demonstrates how this regularity persists in nature’s “impurities.”

I did not directly rely on anyone else’s theory, yet upon completing the article, I discovered that my conclusions resonate with several significant works:

• Ilya Prigogine — ”Order out of Chaos”. This Nobel laureate demonstrates how non-equilibrium systems produce regular cycles and resonances; his concept of “structure = fluctuation + feedback” aligns closely with my principle of phase repetition.
• Steven Strogatz — ”Sync”. This book illustrates how pendulums, fireflies, and neurons spontaneously align into a common rhythm, empirically demonstrating my thesis “balance = integer ratio k.”
• Roger Penrose — *”The Road to Reality”. Penrose elaborates on the role of phase and interference in quantum mechanics, and his interpretation of randomness as lost phase information resonates with my section on “quantum noise.”
• Milan M. Ćirković — ”Fractals, Chaos, and the Laws of Nature”. The author systematically shows scale self-similarity from coastlines to galaxy distributions — precisely the lens through which I view “scale” as simple multiplication of the argument.
• Ervin Laszlo — ”The Akashic Experience”. Laszlo discusses a field that defines the unified “music” of the cosmos — an image resonating with my description of the universe as a single phase carousel.

Thus, although I arrived independently at the ideas of N ≠ 0 and the universal ratio of counters, similar motifs — cycles, resonance, self-similarity, and phase interference — have already been discussed in both classical and contemporary studies.

I understand that without experimental proof, any theory remains a hypothesis. Physics demands data, not just elegant ideas. My model is no exception. It exists within the competitive field alongside general relativity and quantum mechanics, both confirmed by thousands of experiments.

Yet let’s admit it: contemporary science still cannot fully explain the nature of time. We know how to measure it, describe it with equations, yet we don’t understand its essence. What fundamentally is the “flow of time”? Why does it change for different observers?

I propose viewing time from a different angle — not as an independent entity, but as a consequence of deeper processes. My model rests on two key principles:

- Time emerges only where there are measurable state changes in a system. No changes — no time.
- The rate of change and interval fixation in space depends on energy.

This model explains without paradoxes:
- Why quantum processes appear instantaneous.
- How black holes “slow down” time.
- Why different biological species perceive time differently.

Testable consequences of the model:
- Dependence of time’s flow rate on local energy density.
- Possible anomalies in ultra-precise clock operation under extreme energy conditions.

I do not claim absolute truth. Instead, I offer a practical tool that:
- Provides a simpler, more intuitive explanation of time’s nature.
- Allows new experimental inquiries.
- Does not contradict established physical laws.

My model aligns beautifully with the ideas of Leibniz (time as order of events), Mach (time as abstraction from movements), and Carlo Rovelli (time disappearing in quantum gravity).

If I’m mistaken — prove me wrong. But if the model is correct, it could bridge classical and quantum physics.

What’s next?

Task: Verify if the frequency of reference clocks changes dramatically when local energy density suddenly changes.

Experiment: Place two optical frequency combs in different cryostats (300 K and 4 K), or inside a powerful laser beam core, and compare frequency drift with 10⁻¹⁸ precision.

Expectation: If phases govern time, the difference will exceed predictions of General Relativity — we will observe a “temperature gravitational potential,” something classical physics doesn’t predict.

Build a “Phase Spectrometer” for Any Cycles:
Create a device measuring not seconds, meters, or kelvins, but only the ratio of phase clicks. The same chip could be a chronometer, thermometer, and spectrometer by merely changing the reference channel.

Rewrite Physics-0 Curriculum:
Start not from Newton’s forces or electrostatics, but from the axiom N ≠ 0 and formula Q = N_obs / N_ref. A student will immediately see degrees, coulombs, and joules as labels for ratios rather than sacred entities. Phase-based thinking instantly clarifies everything, revealing fundamental patterns at a basic perception level of the world and its phenomena.

Seek Resonance Instead of Maximum:
Replace engineering’s principle “more volts, higher RPM” with “precise phase matching.” Turbines, lasers, quantum qubits — all benefit by aligning in pure integer resonance rather than being driven forward blindly.

Chaos as Hidden Harmony:
Capture optical or acoustic “phase maps” of deterministic chaotic systems (Lorenz attractor, double pendulum) to show trajectories as densely periodic wrappings of the fundamental sine, despite apparent chaos.

Cross-disciplinary Experiments — “One Law, Many Devices”:
- Biologists count mitosis phases,
- Economists track market phases,
- Musicians analyze harmonic phases,

All consolidate data into the single ratio N_obs / N_ref, testing prediction accuracy across fields.

Final Invitation:

Phase vision provides a unified language from quanta to civilizations.

If we learn to work directly with phase ratios, discarding redundant intermediate units, we’ll develop more accurate clocks, cleaner resonators, powerful algorithms, and perhaps a new understanding of “past” and “future.”

Everything begins with the first distinction. Beyond that lies only our inventiveness in choosing standards and our courage to experiment where traditional physics remains silent.

© All rights reserved. For inquiries, discussions, or collaboration, please contact me directly at yahorkamarou@gmail.com. 🇺🇦

Any copying, reproduction, or usage of the presented formulas, interpretations, or concepts without explicit attribution to the original source and acknowledgment of my authorship is strictly prohibited.

Theory of Distinction
The Nonzero Law
Distinction Mechanics